監修
京都大学大学院医学研究科 医学統計生物情報学 教授
森田 智視 先生
監修者の所属・役職は2025年4月時点の情報です
仮説検定
仮説検定
仮説検定とは、解析のために設定した統計的な仮説が正しいかどうかを、集められたデータを用いて確かめる統計手法です。統計学的検定は次の①~④の手順で行われます。
- 帰無仮説を設定する
- 有意水準を設定する
- データを集める
- P値を計算し、P値が有意水準を下回るかどうかを判定する
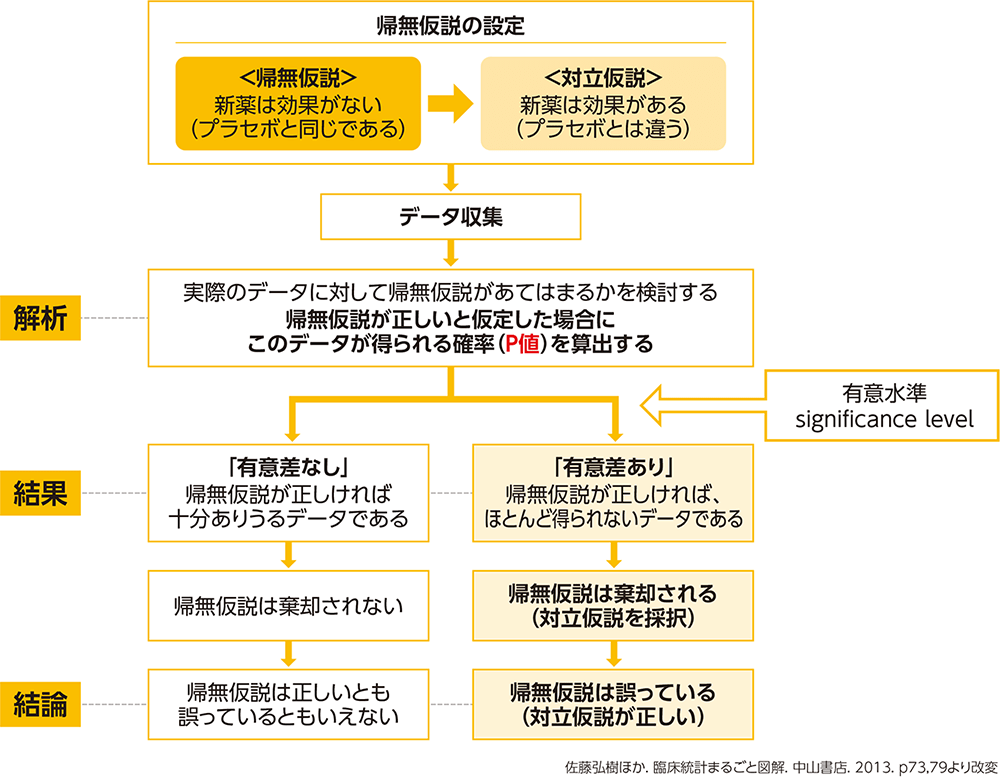
仮説検定では、帰無仮説を否定(棄却)することで対立仮説を主張しますが、その指標として使われるのがP値です。帰無仮説を棄却する基準となる値を有意水準(significance level)といい、一般的に5%が使われます。
P値
統計的仮説検定では、結果の差が偶然によって生じたと考えられる確率を「P値」で表します。P値が有意水準よりも小さい値であれば(一般的にP<0.05)、偶然による結果である可能性が低いと考え「有意差あり」と判断します。「有意差あり」で帰無仮説は棄却され対立仮説が正しいと結論づけられます。一方、「有意差なし」では帰無仮説が正しい、すなわち群間に違いがないとはいえないことに注意が必要です。
P値の誤った解釈
P値には、新薬群と対照群の効果差だけでなく症例数の大きさも影響してきます。多くの症例数を集めることで臨床的に意味がないような差でも「統計的に有意差あり」となることがあります。一方で、症例数が少なすぎることで臨床的に意味があるような差でも「統計的に有意差なし」となることも起こりえます。
参考:代田浩之監修. ここから学ぼう! 図解 医療統計. 総合医学社. 2016, p90-91
新谷歩. 今日から使える医療統計.医学書院. 2015, p15-17
山崎力ほか. 臨床研究いろはにほ. ライフサイエンス出版. 2015, p52-53
佐藤弘樹ほか. 臨床統計まるごと図解. 中山書店. 2013, p70-73, 78-79
仮説検定におけるエラー
仮説検定のエラー
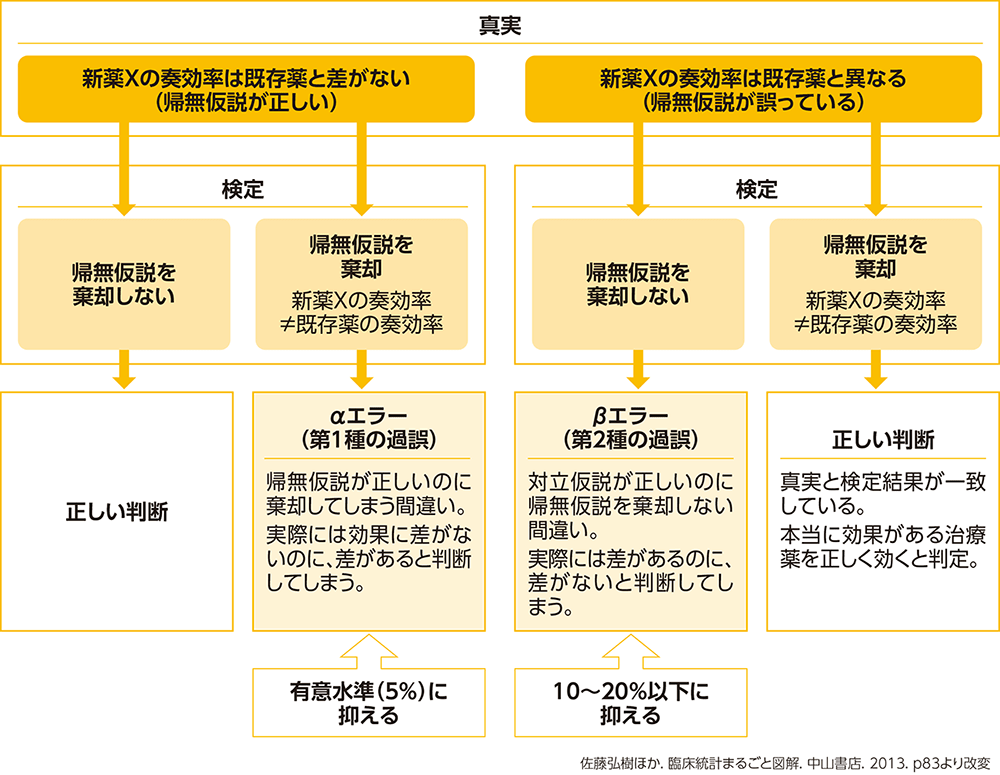
統計的検定は観察されたデータをもとに「推測」を行う作業であるため、いつも正しい判断ができるわけではありません。本当は群間差がないのに統計的に群間差ありといってしまうαエラー(あわてもののエラー、第1種の過誤、type Ⅰ error)と、本当は群間差があるのにその差を見逃してしまうβエラー(ぼんやりもののエラー、第2種の過誤、type Ⅱ error)の2つがあります。
両方のエラーを同時に小さくすることが理想ですが、αエラーを小さくするとβエラーは大きくなる、βエラーを小さくするとαエラーが大きくなるという関係があります。新薬などの開発を行う臨床試験では、差がないものを差があるといってしまうαエラーのほうを重視して、αエラーを設定し、次にβエラーが十分小さくなるように症例数を設定します。αエラーを5%に設定するのが標準で、βエラーは10~20%に設定します。
検出力と症例数
検出力は、1からβエラーを引いた1-βになります。検出したい群間差とその群間差を示すために測定するデータのばらつきを設定し、検出力が80%や90%になるように必要症例数を計算します。これがいわゆるサンプルサイズ(症例数)の設定になります。
参考:代田浩之監修. ここから学ぼう! 図解 医療統計. 総合医学社. 2016, p95-97
新谷歩. 今日から使える医療統計.医学書院. 2015, p66
佐藤弘樹ほか. 臨床統計まるごと図解. 中山書店. 2013, p82-83













